70以上 grain size yield strength equation 251991-How to find the yield strength
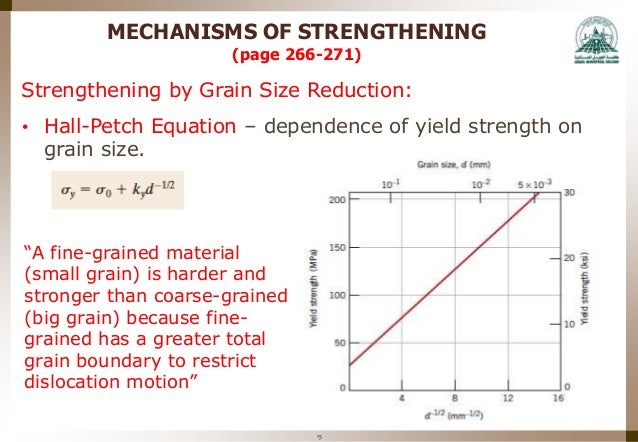
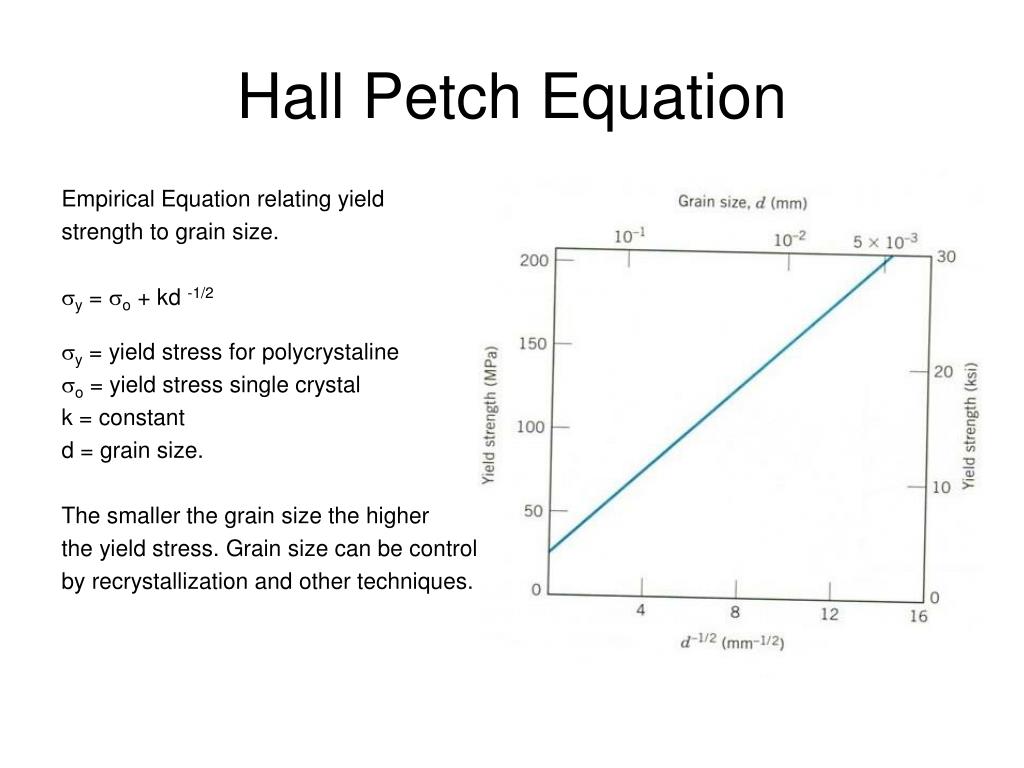
The grain size has an important effect on the mechanical properties of a metal The size of the grains depends upon a number of factors, but the principal one is the heat treatment to which the metal has been subjected When a low carbon steel is heated, there is no change in grain size upto the *lower critical point and it is same for allSizes, the values of typical mechanical properties increase with the reciprocal root of the grain size The classic HallPetch equation relates the yield strength to the grain size σ y = σ 0 Kyd1/2 (1) where Ky is the HallPetch slope and d is the mean grain size An identical relation holds for theStrengthening by Reduction of Grain Size The HallPetch equation describes dependence of yield strength, ς y, as a function of average grain diameter, d The ς 0 is the Peierls (frictional) stress and is the minimum stress needed to induce dislocation glide in a single crystal and k y is the Hall–Petch slope •
What Is The Effect Of Grain Structure On The Properties Of The Material Quora
How to find the yield strength
How to find the yield strength-•This equation indicates that the yield strength has an inverse square root relation with grain size (d) •Theoretically, a material can be made infinitely strong if the grains are made infinitely small s yield = s o k y d 1/2Stress (whereas the HallPetch formula is already in terms of macroscopic yield stress) 104 105 106 107 108 109 1010 1011 1 10 100 1000 104 105 106 creepstrengthhwk4F02Kdata Orowan stress = Gb/l HallPetch = s friction kd1/2 Flow Stress (Pa) Grain Size (nm) Crossover grain size = 144 nm 2b


Why Nanocomposites
Thus, although yield strength is maximized with decreasing grain size, ultimately, very small grain sizes make the material brittle Considered in tandem with the fact that the yield strength is the parameter that predicts plastic deformation in the material, one can make informed decisions on how to increase the strength of a materialThough the values of ΔK associated with these transition points (ΔKT) for an individual steel may tend to exhibit a functional dependence on yield strength (σys) or grain size (¯ℓ)—as is the case, for example, with a lowcarbon ferritic steel—it is unmistakably clear that for the gamut of steels examined (15 cases), the transitionYield_strength_Matcalc Read online for free Scribd is the world's largest social reading and publishing site Open navigation menu Close suggestions Search Search en Change Language close menu
Rather, values of ΔKT for the gamut of steels order on the basis of a synergetic interaction of σys and ¯ℓ, according to the equation, Δ K T = 55 σ y s ℓ ¯ This relationship was derived in the cyclic plastic zone model of fatigue crack growth established in our prior work with titanium alloysWith decreasing grain size Machinability is also affected;The relationship between grain size and yield strength is given by equation 21, known as HallPetch equation Where 𝜎𝑦 is yield strength, 𝜎𝑜 is the friction stress opposing dislocation motion, and K is the stress intensity factor and d is the mean grain size 𝜎𝑦 = 𝜎𝑜 𝐾 𝑑 (21)
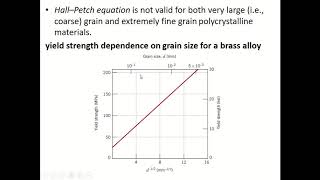
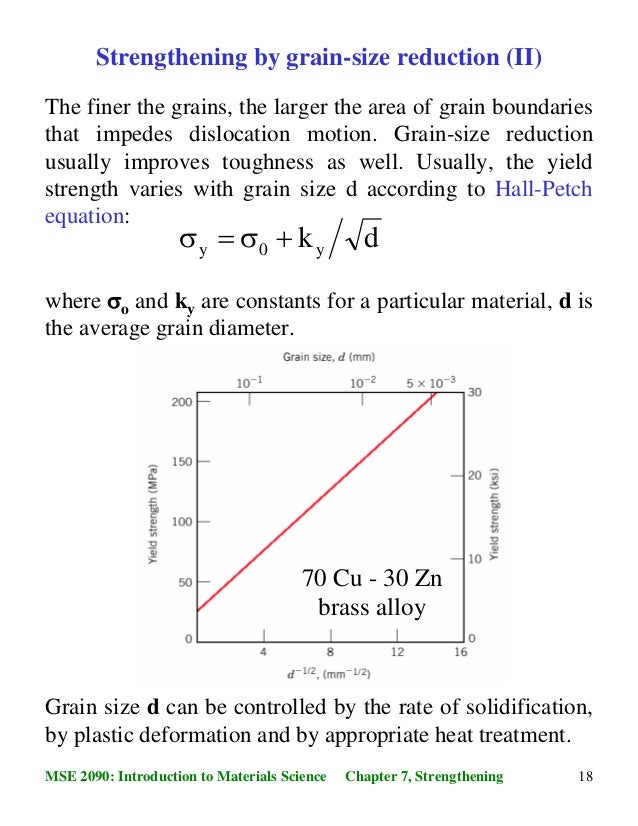
Example Grain Size Strengthening • 70wt%Cu30wt%Zn brass alloy σyield =σo kyd −1/2 • Data grain size (mm)05 σ yield (MPa) 50 100 150 0 0 4 8 12 16 101 2 5x103 grain size, d (mm) 1 ky 0 075mm Kasetsart University DrPeerapong Triyacharoen Department of Materials Engineering Strengthening 138 Solid SolutionGrain Size Reduction • Grain boundaries are barriers to slip • Barrier "strength" increases with misorientation • Smaller grain size more barriers to slip • HallPetch Equation g r a i n b o u n d a r y slip plane grain A g r a i n B σyield =σo kyd −1/2 Note not valid for both very large grain and extremely fine grain materialsOver the range of conventional grain sizes, the values of typical mechanical properties increase with the reciprocal root of the grain size The classic HallPetch equation relates the yield strength to the grain size σy= σ0 Kyd1/2(1) where Kyis the HallPetch slope and d is the mean grain size



Ppt Grain Boundary Strengthening Hall Petch Strengthening Powerpoint Presentation Id


Asmedigitalcollection Asme Org Manufacturingscience Article Pdf 131 1 1 Pdf
Grain size and the above planar measures is also illdefined It is now common to express grain sizes in terms of a simple exponential equation (Equation 1) n = 2 G 1Worked example problem for grain growth and HallPetch yield strength calculation Materials science engineering tutorial solutionStrengthening by Reduction of Grain Size The HallPetch equation describes dependence of yield strength, ς y, as a function of average grain diameter, d The ς 0 is the Peierls (frictional) stress and is the minimum stress needed to induce dislocation glide in a single crystal and k y is the Hall–Petch slope •



Hall Petch Relationship An Overview Sciencedirect Topics


Why Nanocomposites
Assuming that the grain size is Dng and the thickness of grain boundary layer is tg, then the relationship between the thickness of grain boundary and the grain size can be described by the following equation (132)tg = kDng(0 < n < 1) where k and n are regarded as constants for a specific material@article{osti_, title = {The Influence of Grain Size on the Mechanical Properties of Steel}, author = {Morris, J W}, abstractNote = {Many of the important mechanical properties of steel, including yield strength and hardness, the ductilebrittle transition temperature and susceptibility to environmental embrittlement can be improved by refining the grain size2) The equation for the effect of grain size on yield strength is given by σy = σI kD05 where σy is the yield stress, σI is the intrinsic resistance of the lattice to dislocation motion, k is the "blocking parameter" which measures the effectiveness of grain boundaries in blocking dislocation motion, and D is the grain diameter


What Is The Effect Of Grain Structure On The Properties Of The Material Quora


Mme 323 Materials Science Week 7 8 Dislocations Strenghtening M
The dependence of fracture appearance transition temperature (FATT) on phosphorus grain boundary segregation, yield strength, and grain size is experimentally evaluated for a 225Cr–1Mo low‐alloy steel Both the phosphorus boundary segregation and yield strength are directly correlated to the FATT of the steelFerriticgrain size is important sometimes, such as in very low carbon steels, or in ferritic types of alloy steels, or now HSLA steels because the properties of these steels arc strongly effected by the ferritic grain size and is thus measured Hall Petch equation (240) can be applied to obtain the yield strength of these steelsThis is consistent with the observed HallPetch grainsize relationship, whereby the elevation in yield strength due to grainboundary strengthening varies as d − 1/2 We note in passing that Nix has shown that the grainsize effect on strength is enhanced when the material exists in the form of a thin layer on an elastic substrate (Nix, 19)



Mechanisms Of Strengthening In Metals By Harry Liu Medium



Dependence Of Hardening Expressed By The Yield Point R P 0 2 On The Download Scientific Diagram
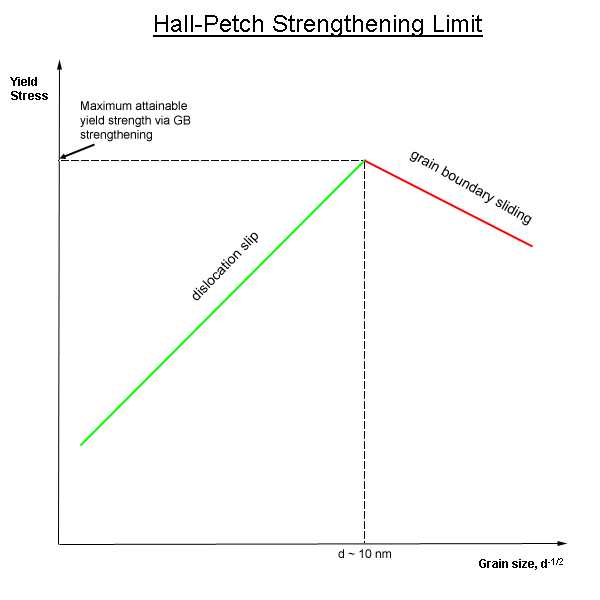
For many materials, the yield strength σ varies with grain size according to σ y = σ y,0 k/d x In this expression, termed the Hall–Petch equation, k is a constant, d is the average grain diameter and σ y,0 is the original yield stress Note that this equation is not valid for both very large (ie, coarse) grain and extremely fineThe HallPetch equation relates the yield strength {sigma} {sub y} of polycrystals to their grain size d {sigma} {sub y} = {sigma} {sub o} k d {sup {minus}1/2}, k is often referred to as the HallPetch slope In a plot {sigma} {sub y} versus d {sup {minus}1/2}, the ordinate intercept equals {sigma} {sub y}6 2𝑑−𝑑𝑜 2= 𝑘𝑡 (22) The results reported by many researchers indicate that the yield strength increases following the HallPetch equation, but if the grain size reduces to the nanorange grain boundaries start to slide This means that by changing grain size one can affect dislocation movement and yield strength I


Steel Material Properties Steelconstruction Info



Steel Properties At Low And High Temperatures Total Materia Article
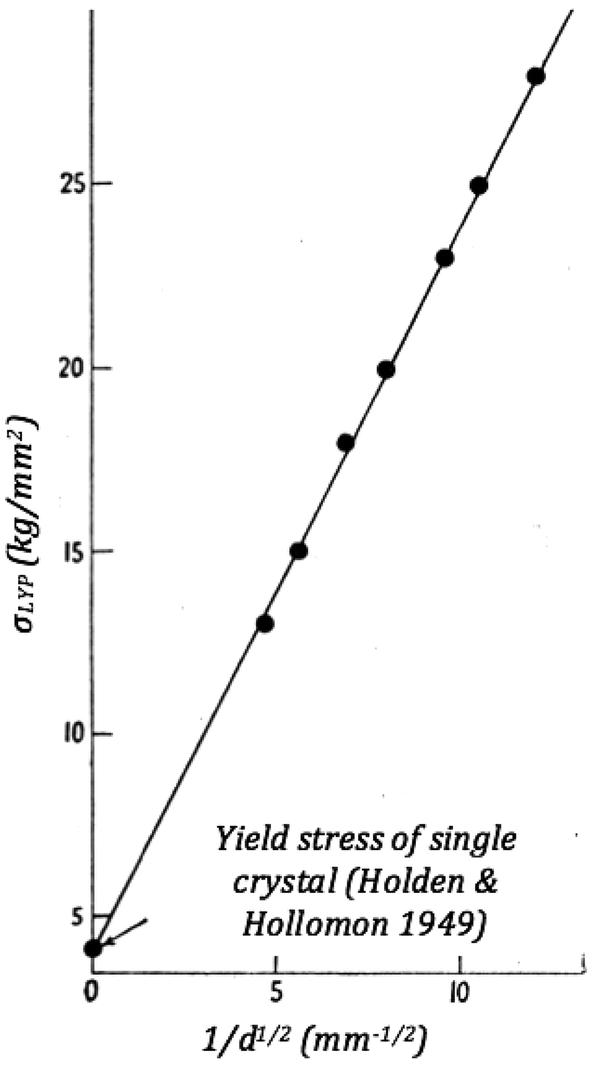
(1) 560 = Sigma0 Ky (0054)^1/2 (2) 7 = Sigma0 Ky (0037)^1/2 (3)160 = Ky (05) Ky=160/035 = 560 ()0037^1/2 = 361 *0045^1/2 = 7 (^1/2 = 1 1 ()0037^1/2 = 1137Grain boundaries For the case of solid solution strengthening, it is shown that existing models for solid solution strengthening cannot explain the observed experimental features in a satisfactory way In the case of grain size strengthening it is shown that a simple model seems to give a relatively good description of the experimental dataSize, hardness, and yield strength of AISI 301 stainless steel The yield strength of metals (σ Y ) is proportional to the inverse of the square root of the grain size (D −1 / 2 ) accord


Solved The Hall Petch Equation Is Commonly Used In The Re Chegg Com


2
Temper Grain Size Tensile Strength ksi Yield Strength (05% Ext) ksi Elongation in inches, % 0070 mm 460 140 65 0050 mm 470 150 62 0035 mm 490 170 57 0025 mm 510 190 54 0015 mm 530 2 50 Eight Hard 500 350 43 Quarter Hard 540 400 23Yield_strength_Matcalc Read online for free Scribd is the world's largest social reading and publishing site Open navigation menu Close suggestions Search Search en Change Language close menuBased on grainsize analyses and on interpretation of borehole geophysical logs Leastsquares linear regression analysis of specific yield and specific retention on grainsize characteristics produced five regression equations that can be used to estimate specific retention from grainsize information Specific yield can be cal


Q Tbn And9gcrlqyrn0v5suymhthl8ogot6cn87lssthmrvyuwnk9zjvgeka8i Usqp Cau


Equal Channel Angular Pressing Technique For The Formation Of Ultra Fine Grained Structures
The size of grains affects the strength of any material, including steels, according to the HallPetch equation σ y = σ 0 k d were σ y is the yield stress, σ 0 is a material constant, k is a strengthening coefficient (again function of the material) and d is the average grain size So the smaller the grain size, the higher the strengthWorked example problem for grain growth and HallPetch yield strength calculation Materials science engineering tutorial solutionZhao et al pointed out that cementite particles effectively increase the yield strength―the higher the volume fraction of cementite particles, the larger the yield strength 13) However, as illustrated in Fig 6, 045C steel has a lower σ ys than the other steels, especially when grain size is small (the smallest grain size corresponds to



Chsc Ch 7 Callister Flashcards Quizlet


Grain Boundary Strengthening Wikipedia
Grain Size and Material Strength (continued) Most metal manufacturers will attempt to keep grain size to a minimum when manufacturing materials for use in electrical connectors A fine grain size will certainly improve the yield strength and stress relaxation resistance of the finished productIn addition to strength, grain size will also effect formability, directionality, texture and surface appearance Table 1 shows the effect of change in grain size on tensile strength, yield strength and elongation Table 1 Annealed Tempers Mechanical Properties, Alloy C Flat Products, Thickness 004 inches;Thus, although yield strength is maximized with decreasing grain size, ultimately, very small grain sizes make the material brittle Considered in tandem with the fact that the yield strength is the parameter that predicts plastic deformation in the material, one can make informed decisions on how to increase the strength of a material



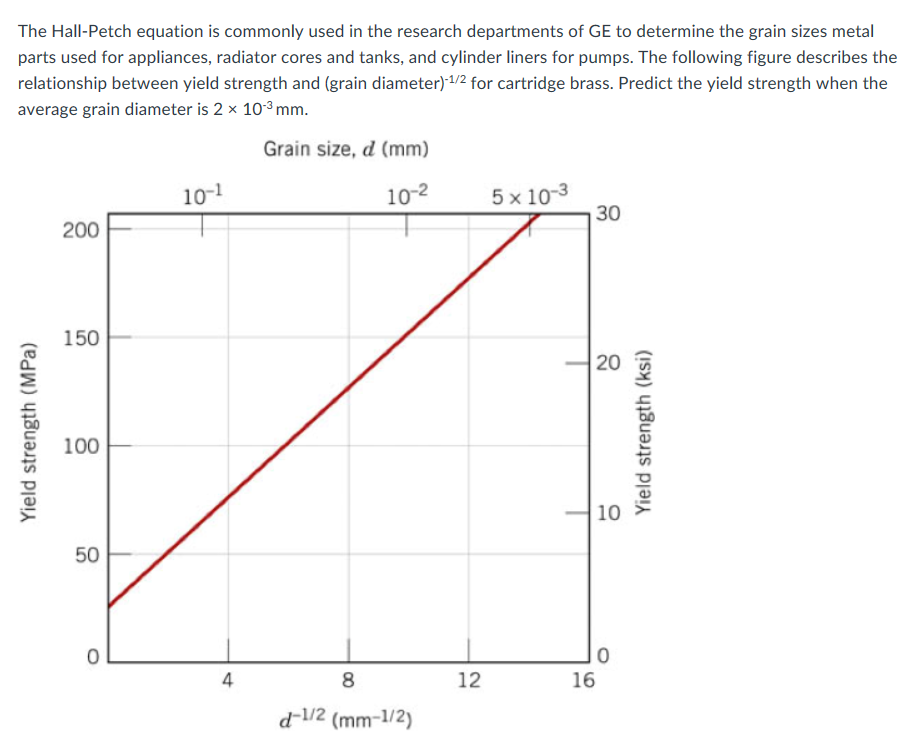
The Following Data Are Obtained In Tension Tests Of Brass Does The Material Follow The Hall Petch Equation Plot Yield Strength Versus Grain Size If So What Is The Value Of K



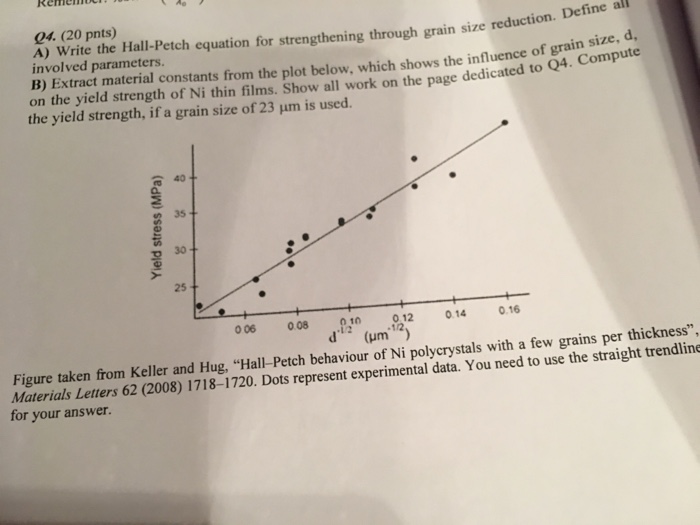
Solved Hi I Am Trying To Solve Q4 Below But I Don T Und Chegg Com
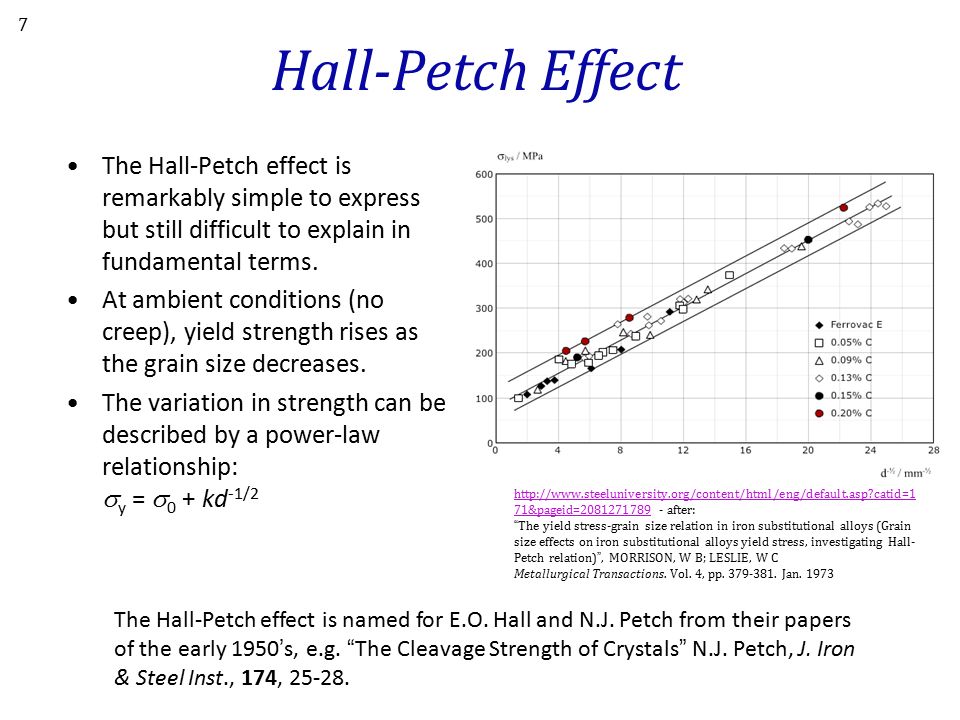
The latter effect is rather interesting, for it implies a question of whether TiAl obeys to the HallPetch equation, which is known to related yield strength to grain size At the same time, the TiAl yield strength largely depends on the slip character which, in its turn, is determined by the grain size and grain boundary structureLower yield strength that Hall expected to see was confirmed (The difference between them decreased to zero when grain size increased to 004 mm) The similarity between the behaviors of cleavage and yield strength was attributed to the f act that yield strength i nvolves shear stresses while cleavage involves normal stressesThe relation between yield stress and grain size is described mathematically by the Hall–Petch equation σ y = σ 0 k y d {\displaystyle \sigma _{\text{y}}=\sigma _{0}{k_{\text{y}} \over {\sqrt {d}}}}



Solutions To Homework 5 Docx Solutions To Homework 5 5 6 Q Can You Suggest A Quick Technique To Check Weather Lines Observed In An Optical Microscope Course Hero


Http Www Me Unm Edu Khraishi Me370 Engr Mat Sci Fall02 Test2 2 Pdf
Details of grain size, twin spacing, yield strength, tensile strength, strain at tensile strength and tensile strain to failure Also included are the strain rate sensitivity exponent, m, determined at different strain rates from the uniaxial tensile tests and strain rate jump tests 9 A clear effectThis was the first chart (eight pictures) to define grain size in terms of the now familiar ASTM grain size numbers (1 to 8 in this chart) Methods E also marked the first detailed description of the Heyn intercept method with equations and a conversion approach to yield ASTM grain size numbersRough machining favors coarse grain size while finish machining favors fine grain size The effect of grain size is greatest on properties that are related to the early stages of deformation Thus, for example, yield stress is more dependent on grain size than tensile strength 2, 3


Http Www Eng Uc Edu Beaucag Classes Properties of materials Homework 11 Answershw2 Pdf



Relationship Between Yield Strength And Grain Size For A Bimodal Structural Ultrafine Grained Ferrite Cementite Steel Sciencedirect
Worked example problem for Hall Petch strength vs grain size Material Science tutorialIn general terms, as grain size increases, the yield and ultimate tensile strengths of a metal are reduced The yield strength σy, is related to the grain size by the Hall–Petch equation σ σ σ y = σ I k y d − 1 / 2 where d is the average grain diameter, and σ I and ky are constants for the metalWith decreasing grain size Machinability is also affected;


Grain Boundary Strengthening Wikipedia


Http Scitation Aip Org Doi Pdf 10 1063 1
This equation relates a material's grain size to its yield strength σy = σ0 Kd1/2 In the Arrhenius equation Co is a constant, R is the gas constant, T is the absolute temperature (K), and Q is the _____ energy required to cause one mole of atoms or ions to moveDOI / Corpus ID Effects of preferred orientation on the grain size dependence of yield strength in metals @article{Wilson1963EffectsOP, title={Effects of preferred orientation on the grain size dependence of yield strength in metals}, author={D Wilson and J A Chapman}, journal={Philosophical Magazine}, year={1963}, volume={8}, pages={} }Severe plastic deformation (SPD) has been widely employed to refine the grain size of Mg alloys, with the main objective to improve the strength and ductility of Mg alloys, since the wellknown HallPetch equation suggests that a decreased grain size leads to an increased yield strength However, the yield strength of Mg alloys processed by SPD is often decreased even though the grain size is
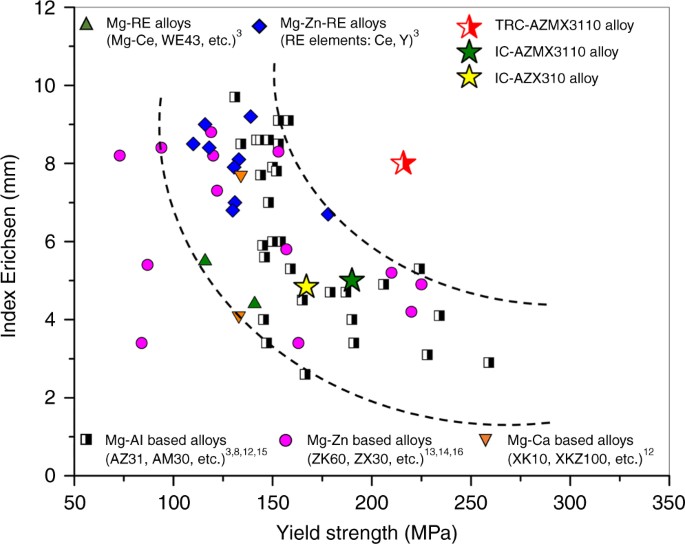


Designing A Magnesium Alloy With High Strength And High Formability Nature Communications
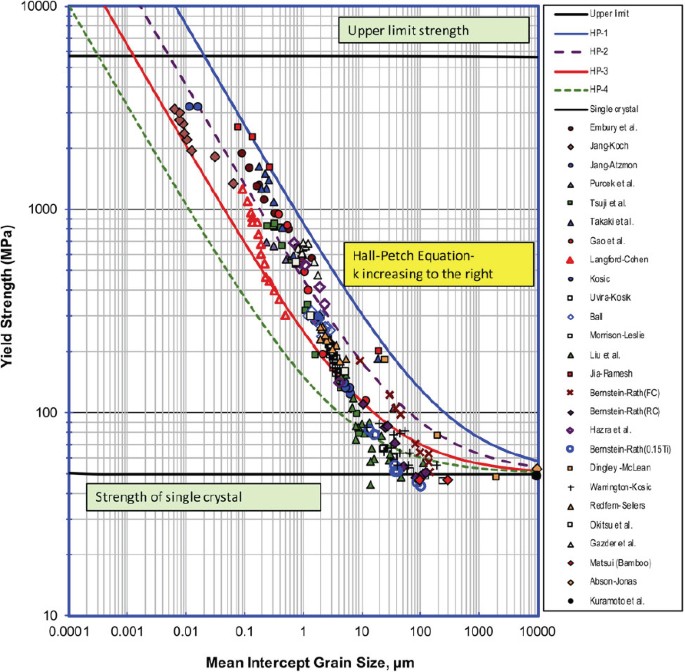


A New Exponential Function To Represent The Effect Of Grain Size On The Strength Of Pure Iron Over Multiple Length Scales Springerlink
Discovered empirical equation that use to predict yield strength is shown in Equations (8, and 9) and constant values (A, A1, , A3, B, C, B1, B2, , C, C1, C2, and C3) are presented in Table 5 which was generated by the data fit program The relationship between yield strength and grain size is shown in Figure 6Rough machining favors coarse grain size while finish machining favors fine grain size The effect of grain size is greatest on properties that are related to the early stages of deformation Thus, for example, yield stress is more dependent on grain size than tensile strength 2, 3The governing formula for this mechanism is is the grain size Theoretical yield strength Material Theoretical shear strength (GPa) Experimental shear strength (GPa) Ag 10 037 Al 09 078 Cu 14 049 Ni 26 32 αFe 26 275 The theoretical yield strength of a perfect crystal is much higher than the observed stress at the initiation of



Hall Petch Relation



Solved Thompson17 Obtained The Following Results For The Yield Stress Of 1 Answer Transtutors



Chapter 7 Dislocation And Strengthening Mechanism Ppt Video Online Download


2


2



Grain Boundary Strengthening Hall Petch Strengthening Ppt Video Online Download



S 2 Marks An Alloy With An Average Grain Diameter Of 35 Um Has A Yield Homeworklib



Solidification Of Mg Zn Zr Alloys Grain Growth Restriction Dendrite Coherency And Grain Size



Hall Petch Equation Strength Vs Grain Size Example Problem Youtube



The Following Data Are Obtained In Tension Tests Of Brass Does The Material Follow The Hall Petch Equation Plot Yield Strength Versus Grain Size If So What Is The Value Of K


The Influence Of Grain Size On The Mechanical Properties Of Steel Welcome To The Publication Archive
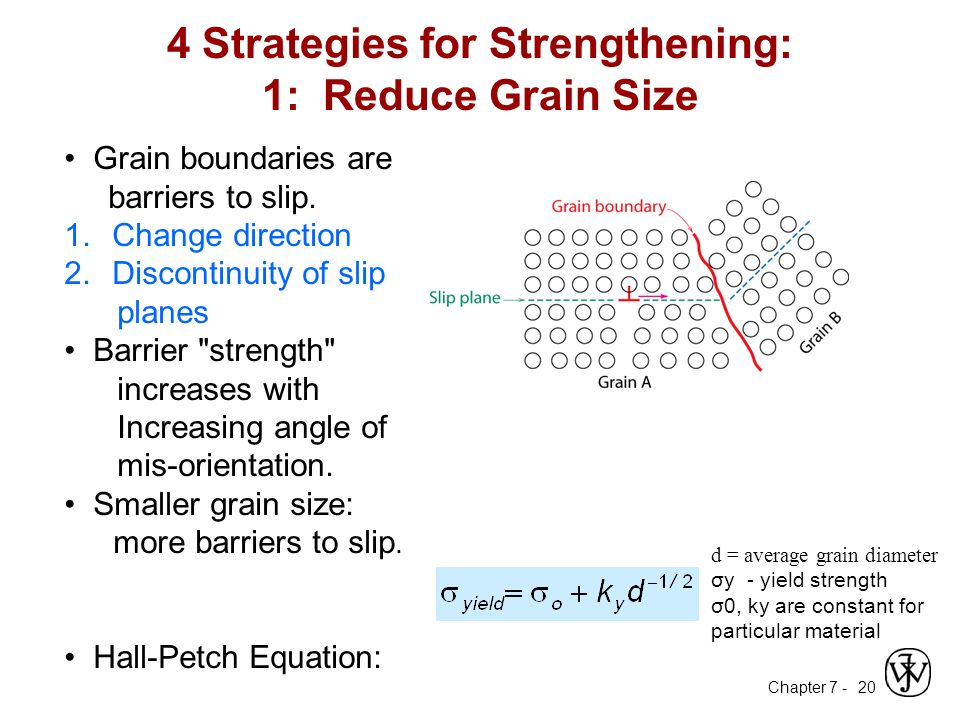


Chapter 7 Dislocations Strengthening Mechanisms Ppt Video Online Download


The Hall Petch And Inverse Hall Petch Relations And The Hardness Of Nanocrystalline Metals Springerlink



How Does The Yield Strength Increase If The Grain Size Is Reduced Quora


Asyn Lec 10 Hall Petch Equation Youtube


Solved Write The Hall Petch Equation For Strengthening Th Chegg Com


2


Pdfs Semanticscholar Org F64c 176f2b76c81d85ab8ee3f976e459c0727e4e Pdf


Zenodo Org Record Files Pdf



Chapter Outline Dislocations And Strengthening Mechanisms Pdf Free Download


Dislocations And Strengthening Mechanisms


Work Hardening Wikipedia


Nanomechanics Mit Edu Sites Default Files Documents 11 Acta Mater Zhu Ntcu Model Pdf


Pdfs Semanticscholar Org F64c 176f2b76c81d85ab8ee3f976e459c0727e4e Pdf


Q Tbn And9gcs 8lrzd0hnah4jrygajql1pckg4c9ugqeg6xh663lvmsta7lba Usqp Cau



Asyn Lec 10 Hall Petch Equation Youtube



Relationship Between The Grain Size And The Yield Strength A And The Download Scientific Diagram


2


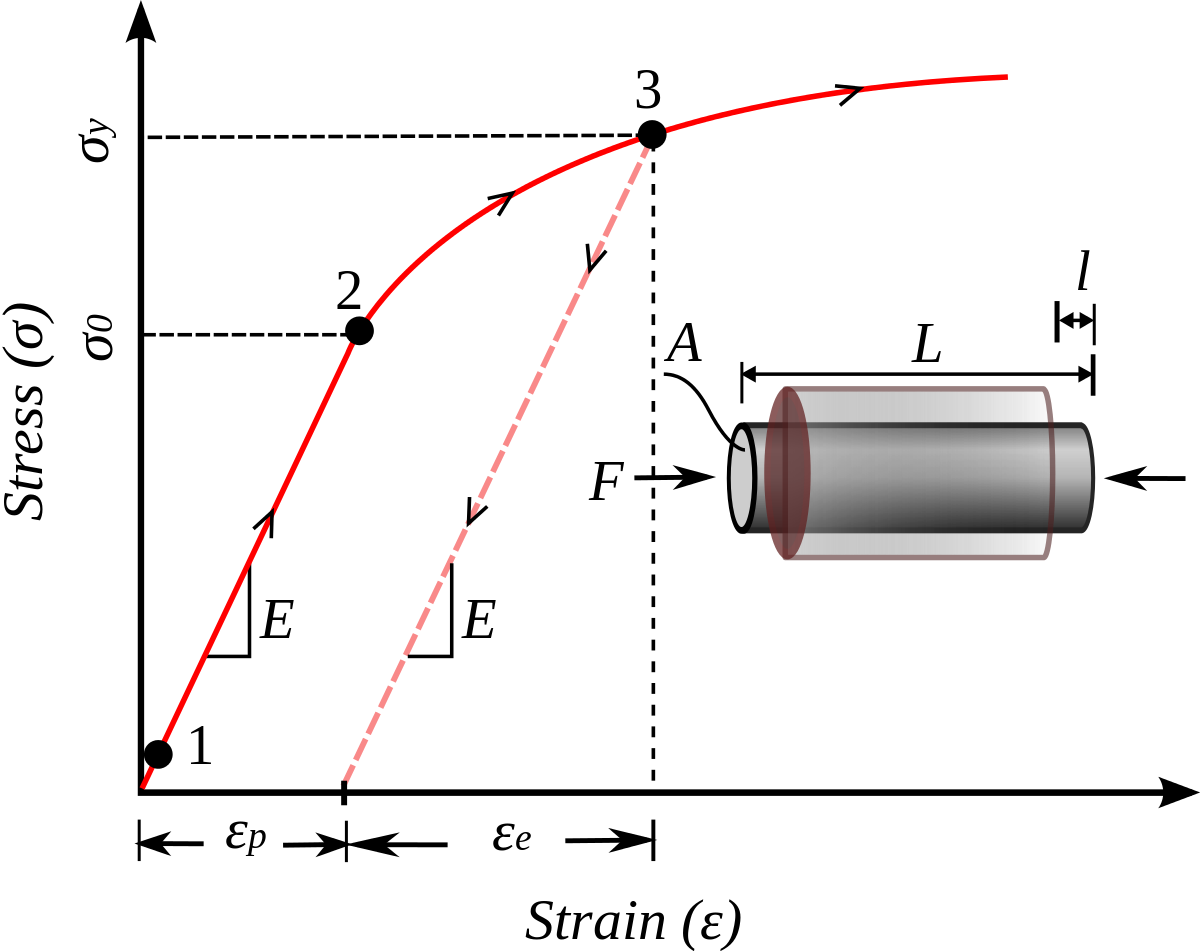
Yield Strength Strength Mechanics Of Materials Engineers Edge


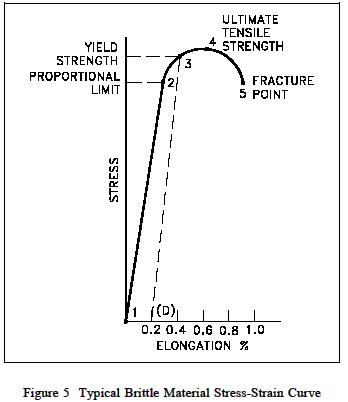
Ppt Che 333 Class 17 Powerpoint Presentation Free Download Id



Yield Point An Overview Sciencedirect Topics


Www Usna Edu Naoe Files Documents Courses En380 Course Notes Ch10 Deformation Pdf


Www2 Gvsu Edu Peirsonb Solidification Yield Strength Pdf
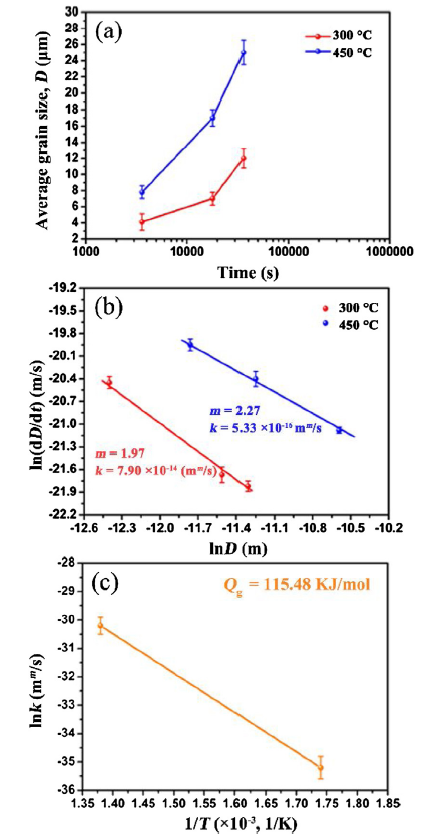


Unveiling Annealing Texture Formation And Static Recrystallization Kinetics Of Hot Rolled Mg Al Zn Mn Ca Alloy


Dspace Mit Edu Bitstream Handle 1721 1 Six decades Pdf Sequence 2 Isallowed Y


Nptel Ac In Content Storage2 Courses Downloads New Noc Mm09 Assigment 7 Pdf
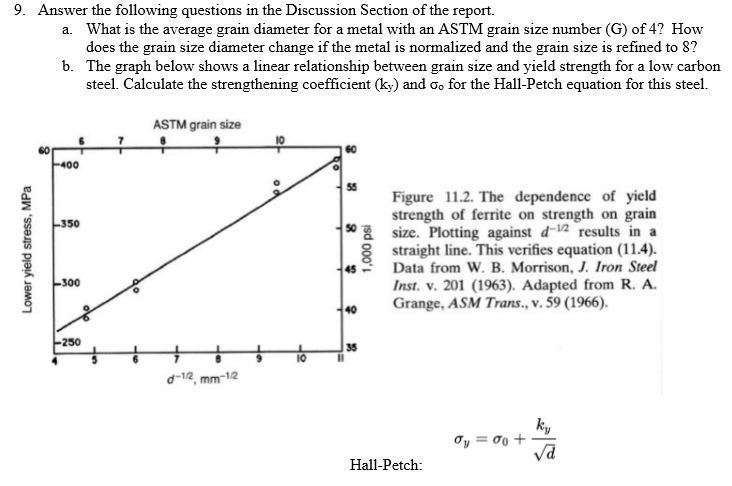


Solved 9 Answer The Following Questions In The Discussio Chegg Com


Evaluation Of Tensile Properties Of Ferrite Single Phase Low Carbon Steel With Different Initial Microstructures



Solved A From The Plot Of Yield Strength Versus Grain Diameter 1 2 1 Answer Transtutors



Mse300 Ppt


Cusn0 5


Microstructure Properties I The Effect Of Grain Size On Strength Creep Resistance A D Rollett M De Graef Updated th Sept Ppt Video Online Download


Materion Com Media Files Alloy Newsletters Technical Tidbits Issue No 15 Grain Size And Material Strength Pdf


Academic Uprm Edu Pcaceres Courses Mechmet Met 6a Pdf



Sol Tema Mec Upc Studocu


Http Www Math Tamu Edu Courses Math151 Matlabspr Week8probs Pdf


2
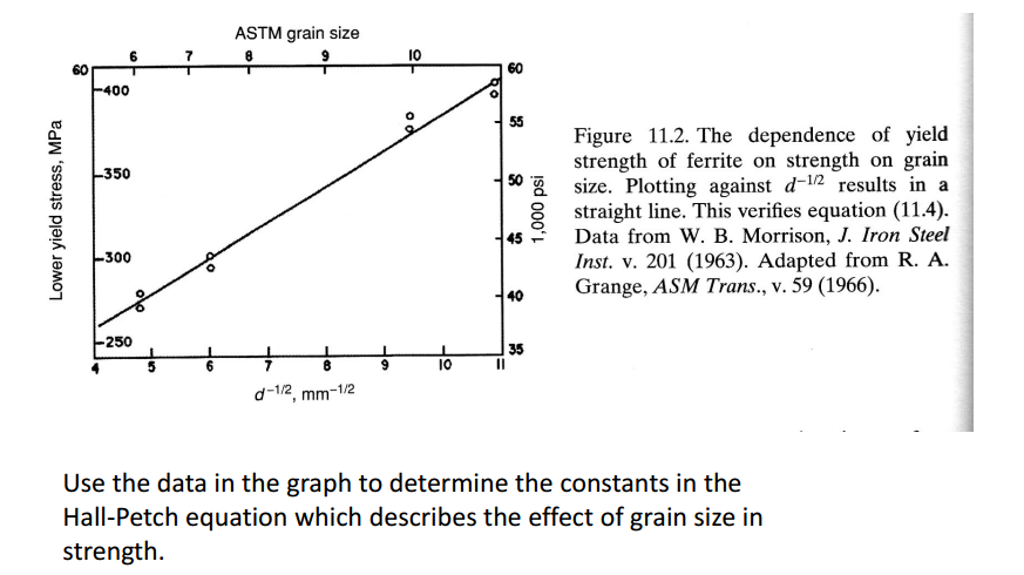


Solved Use The Data In The Graph To Determine The Constan Chegg Com
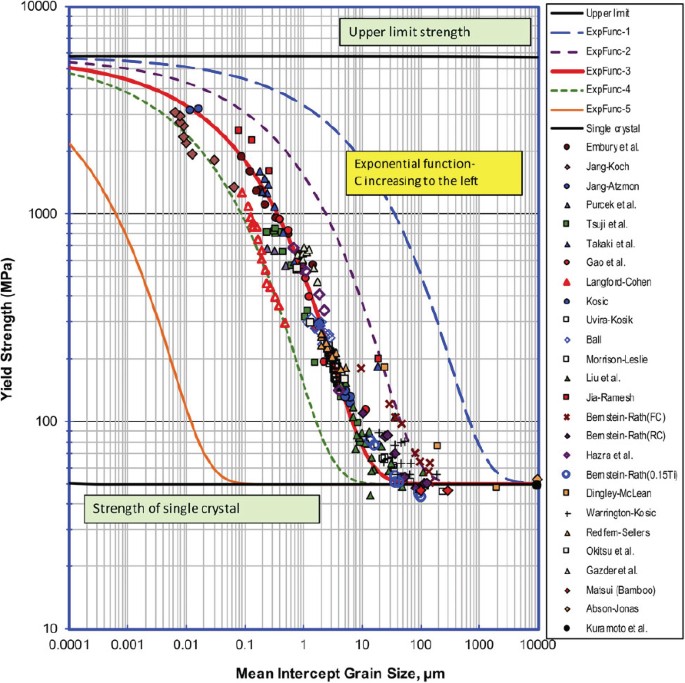


A New Exponential Function To Represent The Effect Of Grain Size On The Strength Of Pure Iron Over Multiple Length Scales Springerlink


2


Mycourses lto Fi Mod Resource View Php Id


Smartech Gatech Edu Bitstream Handle 1853 Jackson Alan N 1978 Ms Pdf


Link Springer Com Content Pdf 10 1007 2f978 3 319 9 74 Pdf


Academic Uprm Edu Pcaceres Courses Mechmet Met 6a Pdf


Www Osti Gov Servlets Purl


Q Tbn And9gcrlqyrn0v5suymhthl8ogot6cn87lssthmrvyuwnk9zjvgeka8i Usqp Cau



Q O Conduction Electrons Texas Powerful Smart



Hall Petch Relationship Between Austenite Grain Size And Yield Download Scientific Diagram
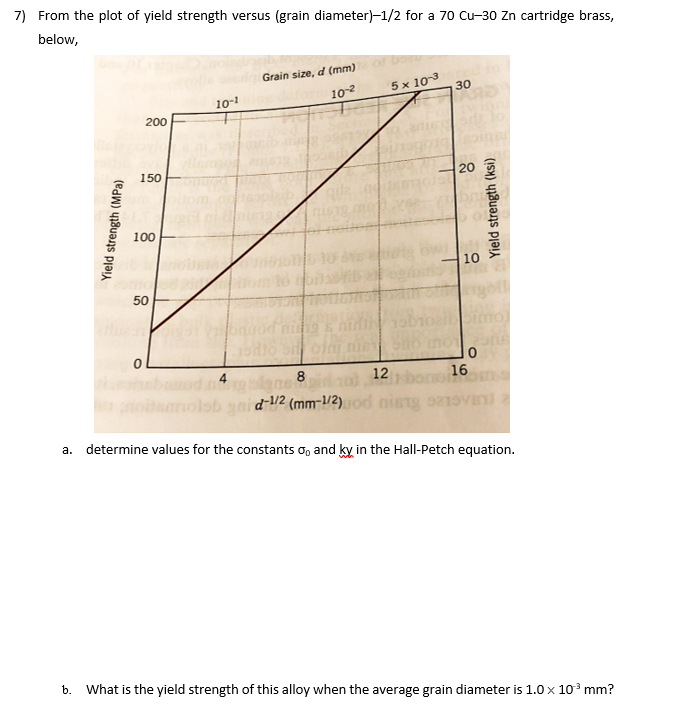


7 From The Plot Of Yield Strength Versus Grain D Chegg Com



How Does The Yield Strength Increase If The Grain Size Is Reduced Quora



Plots Showing Limitation Of Standard Hall Petch Law At Small Grain Download Scientific Diagram



Is There Any Formulae To Calculate The Grain Size Diameter From The Astm Grain Size Number Askmemetallurgy



Step By Step Guide For Grain Size Analysis Geoengineer Org


Cdn Prexams Com 4457 Quiz i Mech340 Solution Pdf



Relationship Between Microstructures And Mechanical Properties Of Ti 6al 4v Alloy In Centrifugal Casting Scientific Net



How Does The Yield Strength Increase If The Grain Size Is Reduced Quora


Www Osti Gov Pages Servlets Purl
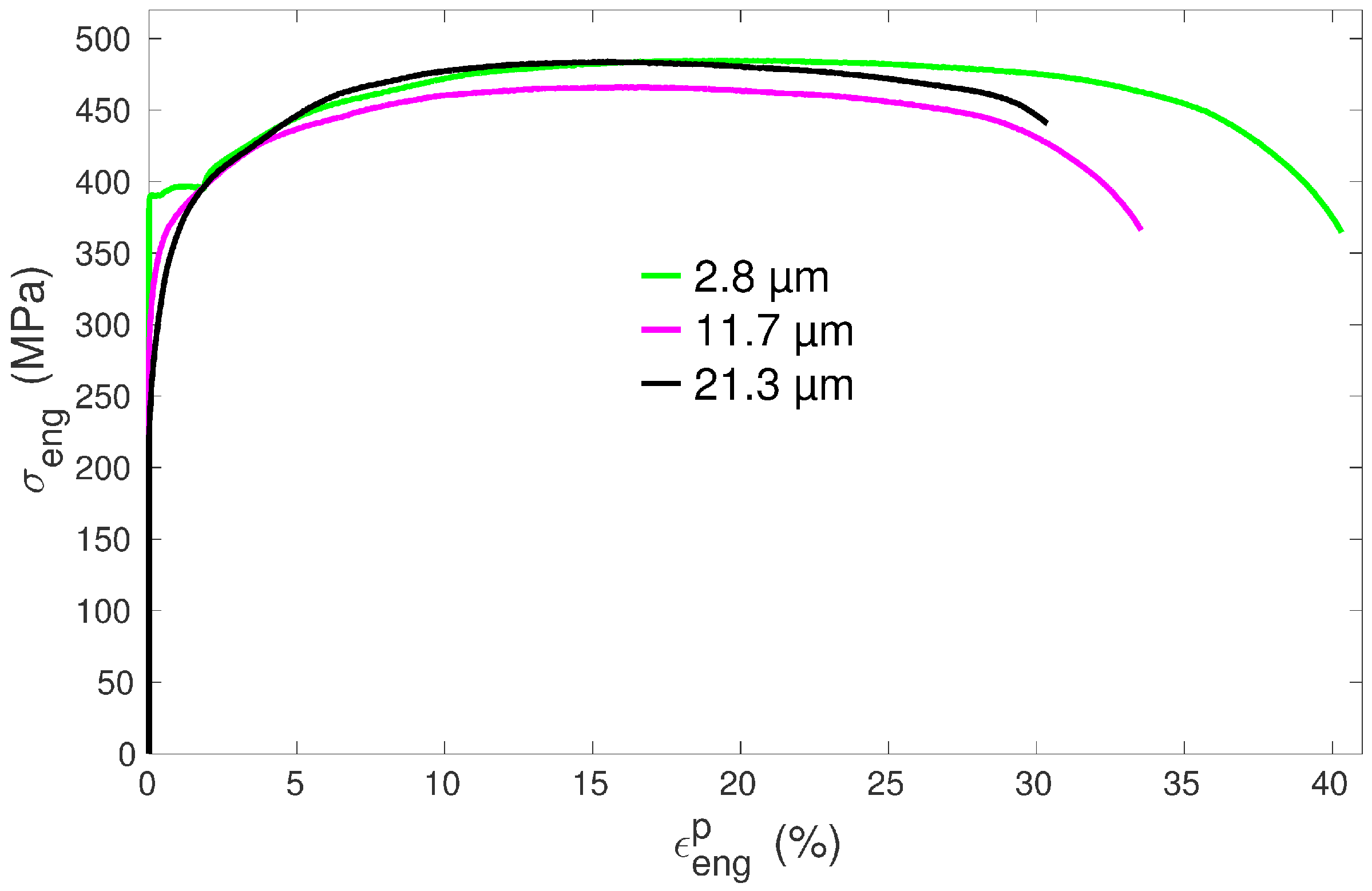


Materials Free Full Text Combined Effects Of Texture And Grain Size Distribution On The Tensile Behavior Of A Titanium
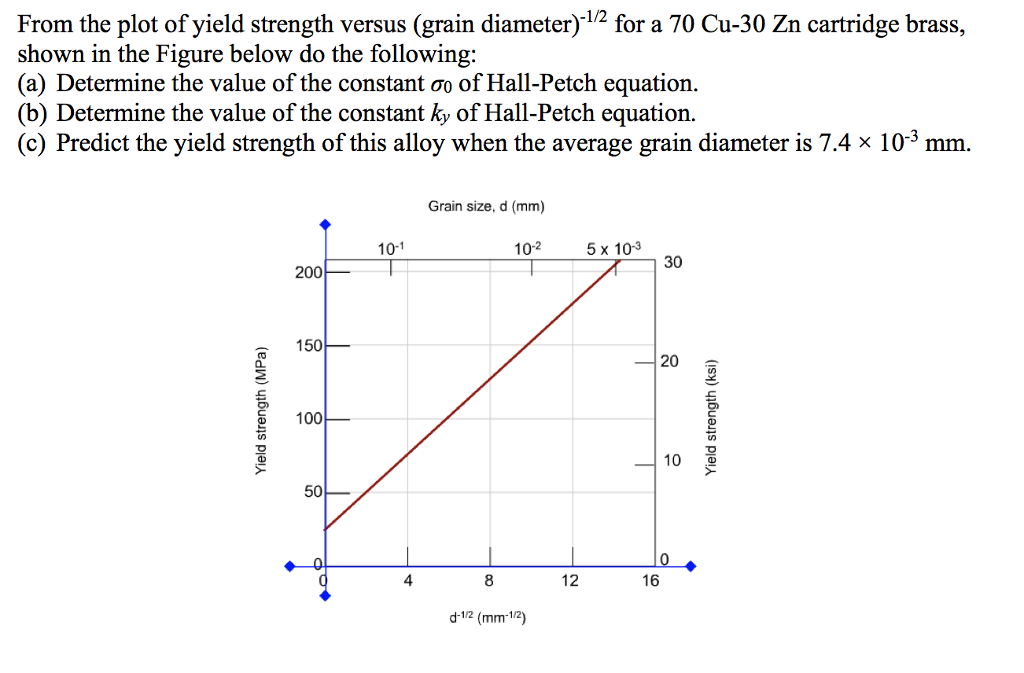


Solved From The Plot Of Yield Strength Versus Grain Diam Chegg Com


Http Meyersgroup Ucsd Edu Papers Journals Meyers 263 Pdf


Http 150 107 117 36 Nptel Disk4 Nptel Contents Web Courses Phase2 Web Module 10 Module 10 Pdf


Www Mdpi Com 2297 8747 2 2 71 Pdf



Journal Of Chemical Engineering And Materials Science A Constitutive Model On Flow Stress Prediction From The Contribution Of Twin And Grain Refinement Strain And Strain Rate During Surface Mechanical Attrition Treatment


Arxiv Org Pdf 1507


2



Chapter 6 Elements Of Grain Boundaries



Yield Engineering Wikipedia


コメント
コメントを投稿